Harmonies of the World (1-5)
Harmonies of the World
by Johannes Kepler
tr. by Charles Glenn Wallis
[1939]
THE HARMONIES OF THE WORLD
by Johannes Kepler
Concerning the very perfect harmony of the celestial movements, and the genesis of eccentricities and the semidiameters, and the periodic times from the same.
After the model of the most correct astronomical doctrine of today, and the hypothesis not only of Copernicus but also of Tycho Brahe, whereof either hypotheses are today publicly accepted as most true, and the Ptolemaic as outmoded.
I commence a sacred discourse, a most true hymn to God the Founder, and I judge it to be piety, not to sacrifice many hecatombs of bulls to Him and to burn incense of innumerable perfumes and cassia, but first to learn myself, and afterwards to teach others too, how great He is in wisdom, how great in power, and of what sort in goodness. For to wish to adorn in every way possible the things that should receive adornment and to envy no thing its goods—this I put down as the sign of the greatest goodness, and in this respect I praise Him as good that in the heights of His wisdom He finds everything whereby each thing may be adorned to the utmost and that He can do by his unconquerable power all that he has decreed.
GALEN, on the Use of Parts. Book III
PROEM
[268] As regards that which I prophesied two and twenty years ago (especially that the five regular solids are found between the celestial spheres), as regards that of which I was firmly persuaded in my own mind before I had seen Ptolemy's Harmonies, as regards that which I promised my friends in the title of this fifth book before I was sure of the thing itself, that which, sixteen years ago, in a published statement, I insisted must be investigated, for the sake of which I spent the best part of my life in astronomical speculations, visited Tycho Brahe, [269] and took up residence at Prague: finally, as God the Best and Greatest, Who had inspired my mind and aroused my great desire, prolonged my life and strength of mind and furnished the other means through the liberality of the two Emperors and the nobles of this province of Austria-on-the-Anisana: after I had discharged my astronomical duties as much as sufficed, finally, I say, I brought it to light and found it to be truer than I had even hoped, and I discovered among the celestial movements the full nature of harmony, in its due measure, together with all its parts unfolded in Book III—not in that mode wherein I had conceived it in my mind (this is not last in my joy) but in a very different mode which is also very excellent and very perfect. There took place in this intervening time, wherein the very laborious reconstruction of the movements held me in suspense, an extraordinary augmentation of my desire and incentive for the job, a reading of the Harmonies of Ptolemy, which had
been sent to me in manuscript by John George Herward, Chancellor of Bavaria, a very distinguished man and of a nature to advance philosophy and every type of learning. There, beyond my expectations and with the greatest wonder, I found approximately the whole third book given over to the same consideration of celestial harmony, fifteen hundred years ago. But indeed astronomy was far from being of age as yet; and Ptolemy, in an unfortunate attempt, could make others subject to despair, as being one who, like Scipio in Cicero, seemed to have recited a pleasant Pythagorean dream rather than to have aided philosophy. But both the crudeness of the ancient philosophy and this exact agreement in our meditations, down to the last hair, over an interval of fifteen centuries, greatly strengthened me in getting on with the job. For what need is there of many men? The very nature of things, in order to reveal herself to mankind, was at work in the different interpreters of different ages, and was the finger of God—to use the Hebrew expression; and here, in the minds of two men, who had wholly given themselves up to the contemplation of nature, there was the same conception as to the configuration of the world, although neither had been the other's guide in taking this route. But now since the first light eight months ago, since broad day three months ago, and since the sun of my wonderful speculation has shone fully a very few days ago: nothing holds me back. I am free to give myself up to the sacred madness, I am free to taunt mortals with the frank confession that I am stealing the golden vessels of the Egyptians, in order to build of them a temple for my God, far from the territory of Egypt. If you pardon me, I shall rejoice; if you are enraged, I shall bear up. The die is cast, and I am writing the book—whether to be read by my contemporaries or by posterity matters not. Let it await its reader for a hundred years, if God Himself has been ready for His contemplator for six thousand years.
The chapters of this book are as follows:
2. On the kinship between them and the harmonic ratios.
3. Summary of astronomical doctrine necessary for speculation into the celestial harmonies.
4. In what things pertaining to the planetary movements the simple consonances have been expressed and that all those consonances which are present in song are found in the heavens.
5. That the clefs of the musical scale, or pitches of the system, and the genera of consonances, the major and the minor, are expressed in certain movements.
6. That the single musical Tones or Modes are somehow expressed by the single planets.
7. That the counterpoints or universal harmonies of all the planets can exist and be different from one another.
8. That four kinds of voice are expressed in the planets: soprano, contralto, tenor, and bass.
[270] 9. Demonstration that in order to secure this harmonic arrangement, those very planetary eccentricities which any planet has as its own, and no others, had to be set up.
10. Epilogue concerning the sun, by way of very fertile conjectures.
Before taking up these questions, it is my wish to impress upon my readers the very exhortation of Timaeus, a pagan philosopher, who was going to speak on the same things: it should be learned by Christians with the greatest admiration, and shame too, if they do not imitate him: Ἀλλ᾽ ὦ Σὼκρατες, τοῦτο γε δὴ πντες ὅσοι καὶ κατὰ βραχὺ σωφροσύνης μετέχουσιν, ἐπὶ πασῇ ὁρμῇ καὶ σμίκροῦ καὶ μεγάλου πράγματος θεὸν ἀει που καοῦσιν. ἡμᾶς δὲ τοὺς περὶ τοῦ πὰντος λόγους ποιεῖσθαι πῃ μέλλοντας. . . , εἰ μὴ πανταπασι παραλλάττομεν, ἀνάγκη θεοὺς τε καὶ θεὰς ἐπικαλουμενους εὔχεσθαι πάντα, κατὰ νοῦν ἐκεῖνοις μἑν μάλιστα, ἑπομένως δέ ἠμῖν εἰπεῖν. For truly, Socrates, since all who have the least particle of intelligence always invoke God whenever they enter upon any business, whether light or arduous; so too, unless we have clearly strayed away from all sound reason, we who intend to have a discussion concerning the universe must of necessity make our sacred wishes and pray to the Gods and Goddesses with one mind that we may say such things as will please and be acceptable to them in especial and, secondly, to you too.
1. CONCERNING THE FIVE REGULAR SOLID FIGURES
[271] It has been said in the second book how the regular plane figures are fitted together to form solids; there we spoke of the five regular solids, among others, on account of the plane figures. Nevertheless their number, five, was there demonstrated; and it was added why they were designated by the Platonists as the figures of the world, and to what element any solid was compared on account of what property. But now, in the anteroom of this book, I must speak again concerning these figures, on their own account, not on account of the planes, as much as suffices for the celestial harmonies; the reader will find the rest in the Epitome of Astronomy, Volume II, Book Iv.
Accordingly, from the Mysterium Cosmographicum, let me here briefly inculcate the order of the five solids in the world, whereof three are primary and two secondary. For the cube (1) is the outmost and the most spacious, because firstborn and having the nature [rationem] of a whole, in the very form of its generation. There follows the tetrahedron (2), as if made a part, by cutting up the cube; nevertheless it is primary too, with a solid trilinear angle, like the cube. Within the tetrahedron is the dodecahedron (3), the last of primary figures, namely, like a solid composed of parts of a cube and similar parts of a tetrahedron, i.e., of irregular tetrahedrons, wherewith the cube inside is roofed over. Next in order is the icosahedron (4) on account of its similarity, the last of the secondary figures and having a plurilinear solid angle. The octahedron (6) is inmost, which is similar to the cube and the first of the secondary figures and to which as inscriptile the first place is due, just as the first outside place is due to the cube as circumscriptile.
[272] However, there are as it were two noteworthy weddings of these figures, made from different classes: the males, the cube and the dodecahedron, among the primary; the females, the octahedron and the icosahedron, among the secondary, to which is added one as it were bachelor or hermaphrodite, the tetrahedron, because it is inscribed in itself, just as those female solids are inscribed in the males and are as it were subject to them, and have the signs of the feminine sex, opposite the masculine, namely, angles opposite planes. Moreover, just as the tetrahedron is the element, bowels, and as it were rib of the male
cube, so the feminine octahedron is the element and part of the tetrahedron in another way; and thus the tetrahedron mediates in this marriage.
The main difference in these wedlocks or family relationships consists in the following: the ratio of the cube is rational. For the tetrahedron is one third of the body of the cube, and the octahedron half of the tetrahedron, one sixth of the cube; while the ratio of the dodecahedron's wedding is irrational [ineffabilis] but divine.
The union of these two words commands the reader to be careful as to their significance. For the word ineffabilis here
 Click to enlarge |
does not of itself denote any nobility, as elsewhere in theology and divine things, but denotes an inferior condition. For in geometry, as was said in the first book, there are many irrationals, which do not on that account participate in a divine proportion too. But you must look in the first book for what the divine ratio, or rather the divine section, is. For in other proportions there are four terms present; and three, in a continued proportion; but the divine requires a single relation of terms outside of that of the proportion itself, namely in such fashion that the two lesser terms, as parts make up the greater term, as a whole. Therefore, as much as is taken away from this wedding of the dodecahedron on account of its employing an irrational proportion, is added to it conversely, because its irrationality approaches the divine. This wedding also comprehends the solid star too, the generation whereof arises from the continuation of five planes of the dodecahedron till they all meet in a single point. See its generation in Book
Lastly, we must note the ratio of the spheres circumscribed around them to those inscribed in them: in the case of the tetrahedron it is rational, 100,000 : 33,333 or 3 : 1; in the wedding of the cube it is irrational, but the radius of the inscribed sphere is rational in square, and is itself the square root of one third the square on the radius [of the circumscribed sphere], namely 100,000 : 57,735; in the wedding of the dodecahedron, clearly irrational, 100,000 : 79,465; in the case of the star, 100,000 : 52,573, half the side of the icosahedron or half the distance between two rays.
2. ON THE KINSHIP BETWEEN THE HARMONIC RATIOS AND THE FIVE REGULAR FIGURES
[273] This kinship [cognatio] is various and manifold; but there are four degrees of kinship. For either the sign of kinship is taken from the outward form alone which the figures have, or else ratios which are the same as the harmonic arise in the construction of the side, or result from the figures already constructed, taken simply or together; or, lastly, they are either equal to or approximate the ratios of the spheres of the figure.
In the first degree, the ratios, where the character or greater term is 3, have kinship with the triangular plane of the tetrahedron, octahedron, and icosahedron;
but where the greater term is 4, with the square plane of the cube; where 5, with the pentagonal plane of the dodecahedron. This similitude on the part of the plane can also be extended to the smaller term of the ratio, so that wherever the number 3 is found as one term of the continued doubles, that ratio is held to be akin to the three figures first named: for example, 1 : 3 and 2 : 3 and 4 : 3 and 8 : 3, et cetera; but where the number is 5, that ratio is absolutely assigned to the wedding of the dodecahedron : for example, 2 : 5 and 4 : 5 and 8 : 5, and thus 3 : 5 and 3 : 10 and 6 : 5 and 12 : 5 and 24 : 5. The kinship will be less probable if the sum of the terms expresses this similitude, as in 2 : 3 the sum of the terms is equal to 5, as if to say that 2 : 3 is akin to the dodecahedron. The kinship on account of the outward form of the solid angle is similar: the solid angle is trilinear among the primary figures, quadrilinear in the octahedron, and quinquelinear in the icosahedron. And so if one term of the ratio participates in the number 3, the ratio will be connected with the primary bodies; but if in the number 4, with the octahedron; and finally, if in the number 5, with the icosahedron. But in the feminine solids this kinship is more apparent, because the characteristic figure latent within follows upon the form of the angle: the tetragon in the octahedron, the pentagon in the icosahedron; and so 3 : 5 would go to the sectioned icosahedron for both reasons.
The second degree of kinship, which is genetic, is to be conceived as follows: First, some harmonic ratios of numbers are akin to one wedding or family, namely, perfect ratios to the single family of the cube; conversely, there is the ratio which is never fully expressed in numbers and cannot be demonstrated by numbers in any other way, except by a long series of numbers gradually approaching it: this ratio is called divine, when it is perfect, and it rules in various ways throughout the dodecahedral wedding. Accordingly, the following consonances begin to shadow forth that ratio: 1 : 2 and 2 : 3 and 2 : 3 and 5 : 8. For it exists most imperfectly in 1 : 2, more perfectly in 5 : 8, and still more perfectly if we add 5 and 8 to make 13 and take 8 as the numerator, if this ratio has not stopped being harmonic.
Further, in constructing the side of the figure, the diameter of the globe must be cut; and the octahedron demands its bisection, the cube and the tetrahedron its trisection, the dodecahedral wedding its quinquesection. Accordingly, the ratios between the figures are distributed according to the numbers which express those ratios. But the square on the diameter is cut too, or the square on the side of the figure is formed from a fixed part of the diameter. And then the squares on the sides are compared with the square on the diameter, and they constitute the following ratios : in the cube 1 : 3, in the tetrahedron 2 : 3, in the octahedron 1 : 2. Wherefore, if the two ratios are put together, the cubic and the tetrahedral will give 1 : 2; the cubic and the octahedral, 2 : 3; the octahedral and the tetrahedral, 3 : 4. The sides in the dodecahedral wedding are irrational.
Thirdly, the harmonic ratios follow in various ways upon the already constructed figures. For either the number of the sides of the plane is compared with the number of lines in the total figure; [274] and the following ratios arise : in the cube, 4 : 12 or 1 : 3; in the tetrahedron 3 : 6 or 1 : 2; in the octahedron 3 : 12 or 1 : 4; in the dodecahedron 5 : 30 or 1 : 6; in the icosahedron 3 : 30 or 1 : 10. Or else the number of sides of the plane is compared with the number of planes; then the cube gives 4 : 6 or 2 : 3, the tetrahedron 3 : 4, the octahedron 3 : 8, the dodecahedron 5 : 12, the icosahedron 3 : 20. Or else the number of
sides or angles of the plane is compared with the number of solid angles, and the cube gives 4 : 8 or 1 : 2, the tetrahedron 3 : 4, the octahedron 3 : 6 or 1 : 2, the dodecahedron with its consort 5 : 20 or 3 : 12 (i.e., 1 : 4). Or else the number of planes is compared with the number of solid angles, and the cubic wedding gives 6 : 8 or 3 : 4, the tetrahedron the ratio of equality, the dodecahedral wedding 12 : 20 or 3 : 5. Or else the number of all the sides is compared with the number of the solid angles, and the cube gives 8 : 12 or 2 : 3, the tetrahedron 4 : 6 or 2 : 3, and the octahedron 6 : 12 or 1 : 2, the dodecahedron 20 : 30 or 2 : 3, the icosahedron 12 : 30 or 2 : 5.
Moreover, the bodies too are compared with one another, if the tetrahedron is stowed away in the cube, the octahedron in the tetrahedron and cube, by geometrical inscription. The tetrahedron is one third of the cube, the octahedron half of the tetrahedron, one sixth of the cube, just as the octahedron, which is inscribed in the globe, is one sixth of the cube which circumscribes the globe. The ratios of the remaining bodies are irrational.
The fourth species or degree of kinship is more proper to this work: the ratio of the spheres inscribed in the figures to the spheres circumscribing them is sought, and what harmonic ratios approximate them is calculated. For only in the tetrahedron is the diameter of the inscribed sphere rational, namely, one third of the circumscribed sphere. But in the cubic wedding the ratio, which is single there, is as lines which are rational only in square. For the diameter of the inscribed sphere is to the diameter of the circumscribed sphere as the square root of the ratio 1 : 3. And if you compare the ratios with one another, the ratio of the tetrahedral spheres is the square of the ratio of the cubic spheres. In the dodecahedral wedding there is again a single ratio, but an irrational one, slightly greater than 4 : 5. Therefore the ratio of the spheres of the cube and octahedron is approximated by the following consonances : 1 : 2, as proximately greater, and
3 : 5, as proximately smaller. But the ratio of the dodecahedral spheres is approximated by the consonances 4 : 5 and 5 : 6, as proximately smaller, and 3 : 4 and 5 : 8, as proximately greater.
But if for certain reasons 1 : 2 and 1 : 3 are arrogated to the cube, the ratio of the spheres of the cube will be to the ratio of the spheres of the tetrahedron as the consonances 1 : 2 and 1 : 3, which have been ascribed to the cube, are to 1 : 4 and 1 : 9, which are to be assigned to the tetrahedron, if this proportion is to be used. For these ratios, too, are as the squares of those consonances. And because 1 : 9 is not harmonic, 1 : 8 the proximate ratio takes its place in the tetrahedron. But by this proportion approximately 4 : 5 and 3 : 4 will go with the dodecahedral wedding. For as the ratio of the spheres of the cube is approximately the cube of the ratio of the dodecahedral, so too the cubic consonances 1 : 2 and 2 : 3 are approximately the cubes of the consonances 4 : 5 and 3 : 4. For 4 : 5 cubed is 64 : 125, and 1 : 2 is 64 : 128. So 3 : 4 cubed is 27 : 64, and 1 : 3 is 27 : 81.
3. A SUMMARY OF ASTRONOMICAL DOCTRINE NECESSARY FOR SPECULATION INTO THE CELESTIAL HARMONIES
First of all, my readers should know that the ancient astronomical hypotheses of Ptolemy, in the fashion in which they have been unfolded in the Theoricae of Peurbach and by the other writers of epitomes, are to be completely removed
from this discussion and cast out of [275] the mind. For they do not convey the true lay out of the bodies of the world and the polity of the movements.
Although I cannot do otherwise than to put solely Copernicus’ opinion concerning the world in the place of those hypotheses and, if that were possible, to persuade everyone of it; but because the thing is still new among the mass of the intelligentsia [apud vulgus studiosorum], and the doctrine that the Earth is one of the planets and moves among the stars around a motionless sun sounds very absurd to the ears of most of them: therefore those who are shocked by the unfamiliarity of this opinion should know that these harmonical speculations are possible even with the hypotheses of Tycho Brahe—because that author holds, in common with Copernicus, everything else which pertains to the lay out of the bodies and the tempering of the movements, and transfers solely the Copernican annual movement of the Earth to the whole system of planetary spheres and to the sun, which occupies the centre of that system, in the opinion of both authors. For after this transference of movement it is nevertheless true that in Brahe the Earth occupies at any time the same place that Copernicus gives it, if not in the very vast and measureless region of the fixed stars, at least in the system of the planetary world. And accordingly, just as he who draws a circle on paper makes the writing-foot of the compass revolve, while he who fastens the paper or tablet to a turning lathe draws the same circle on the revolving tablet with the foot of the compass or stylus motionless; so too, in the case of Copernicus the Earth, by the real movement of its body, measures out a circle revolving midway between the circle of Mars on the outside and that of Venus on the inside; but in the case of Tycho Brahe the whole planetary system (wherein among the rest the circles of Mars and Venus are found) revolves like a tablet on a lathe and applies to the motionless Earth, or to the stylus on the lathe, the midspace between the circles of Mars and Venus; and it comes about from this movement of the system that the Earth within it, although remaining motionless, marks out the same circle around the sun and midway between Mars and Venus, which in Copernicus it marks out by the real movement of its body while the system is at rest. Therefore, since harmonic speculation considers the eccentric movements of the planets, as if seen from the sun, you may easily understand that if any observer were stationed on a sun as much in motion as you please, nevertheless for him the Earth, although at rest (as a concession to Brahe), would seem to describe the annual circle midway between the planets and in an intermediate length of time. Wherefore, if there is any man of such feeble wit that he cannot grasp the movement of the earth among the stars, nevertheless he can take pleasure in the most excellent spectacle of this most divine construction, if he applies to their image in the sun whatever he hears concerning the daily movements of the Earth in its eccentric—such an image as Tycho Brahe exhibits, with the Earth at rest.
And nevertheless the followers of the true Samian philosophy have no just cause to be jealous of sharing this delightful speculation with such persons, because their joy will be in many ways more perfect, as due to the consummate perfection of speculation, if they have accepted the immobility of the sun and the movement of the earth.
Firstly [I], therefore, let my readers grasp that today it is absolutely certain among all astronomers that all the planets revolve around the sun, with the exception of the moon, which alone has the Earth as its centre: the magnitude
of the moon's sphere or orbit is not great enough for it to be delineated in this diagram in a just ratio to the rest. Therefore, to the other five planets, a sixth, the Earth, is added, which traces a sixth circle around the sun, whether by its own proper movement with the sun at rest, or motionless itself and with the whole planetary system revolving.
Secondly [II]: It is also certain that all the planets are eccentric, i.e., they change their distances from the
 Click to enlarge |
sun, in such fashion that in one part of their circle they become farthest away from the sun, [276] and in the opposite part they come nearest to the sun. In the accompanying diagram three circles apiece have been drawn for the single planets: none of them indicate the eccentric route of the planet itself; but the mean circle, such as BE in the case of Mars, is equal to the eccentric orbit, with respect to its longer diameter. But the orbit itself, such as AD, touches AF, the upper of the three, in one place A, and the lower circle CD, in the opposite place D. The circle GH made with dots and described through the centre of the sun indicates the route of the sun according to Tycho Brahe. And if the sun moves on this route, then absolutely all the points in this whole planetary system here depicted advance upon an equal route, each upon his own. And with one point of it (namely, the centre of the sun) stationed at one point of its circle, as here at the lowest, absolutely each and every point of the system will be stationed at the lowest part of its circle. However, on account of the smallness of the space the three circles of Venus unite in one, contrary to my intention.
Thirdly [III]: Let the reader recall from my Mysterium Cosmographicum, which I published twenty-two years ago, that the number of the planets or circular routes around the sun was taken by the very wise Founder from the five regular solids, concerning which Euclid, so many ages ago, wrote his book which is called the Elements in that it is built up out of a series of propositions. But it has been made clear in the second book of this work that there cannot be more
regular bodies, i.e., that regular plane figures cannot fit together in a solid more than five times.
Fourthly [IV]: As regards the ratio of the planetary orbits, the ratio between two neighbouring planetary orbits is always of such a magnitude that it is easily apparent that each and every one of them approaches the single ratio of the spheres of one of the five regular solids, namely, that of the sphere circumscribing to the sphere inscribed in the figure. Nevertheless it is not wholly equal, as I once dared to promise concerning the final perfection of astronomy. For, after completing the demonstration of the intervals from Brahe's observations, I discovered the following: if the angles of the cube [277] are applied to the inmost circle of Saturn, the centres of the planes are approximately tangent to the middle circle of Jupiter; and if the angles of the tetrahedron are placed against the inmost circle of Jupiter, the centres of the planes of the tetrahedron are approximately tangent to the outmost circle of Mars; thus if the angles of the octahedron are placed against any circle of Venus (for the total interval between the three has been very much reduced), the centres of the planes of the octahedron penetrate and descend deeply within the outmost circle of Mercury, but nonetheless do not reach as far as the middle circle of Mercury; and finally, closest of all to the ratios of the dodecahedral and icosahedral spheres—which ratios are equal to one another—are the ratios or intervals between the circles of Mars and the Earth, and the Earth and Venus; and those intervals are similarly equal, if we compute from the inmost circle of Mars to the middle circle of the Earth, but from the middle circle of the Earth to the middle circle of Venus. For the middle distance of the Earth is a mean proportional between the least distance of Mars and the middle distance of Venus. However, these two ratios between the planetary circles are still greater than the ratios of those two pairs of spheres in the figures, in such fashion that the centres of the dodecahedral planes are not tangent to the outmost circle of the Earth, and the centres of the icosahedral planes are not tangent to the outmost circle of Venus; nor, however, can this gap be filled by the semidiameter of the lunar sphere, by adding it, on the upper side, to the greatest distance of the Earth and subtracting it, on the lower, from the least distance of the same. But I find a certain other ratio of figures—namely, if I take the augmented dodecahedron, to which I have given the name of echinus, (as being fashioned from twelve quinquangular stars and thereby very close to the five regular solids), if I take it, I say, and place its twelve points in the inmost circle of Mars, then the sides of the pentagons, which are the bases of the single rays or points, touch the middle circle of Venus. In short: the cube and the octahedron, which are consorts, do not penetrate their planetary spheres at all; the dodecahedron and the icosahedron, which are consorts, do not wholly reach to theirs, the tetrahedron exactly touches both: in the first case there is falling short; in the second, excess; and in the third, equality, with respect to the planetary intervals.
Wherefore it is clear that the very ratios of the planetary intervals from the sun have not been taken from the regular solids alone. For the Creator, who is the very source of geometry and, as Plato wrote, "practices eternal geometry," does not stray from his own archetype. And indeed that very thing could be inferred from the fact that all the planets change their intervals throughout fixed periods of time, in such fashion that each has two marked intervals from the sun, a greatest and a least; and a fourfold comparison of the intervals from the
sun is possible between two planets: the comparison can be made between either the greatest, or the least, or the contrary intervals most remote from one another, or the contrary intervals nearest together. In this way the comparisons made two by two between neighbouring planets are twenty in number, although on the contrary there are only five regular solids. But it is consonant that if the Creator had any concern for the ratio of the spheres in general, He would also have had concern for the ratio which exists between the varying intervals of the single planets specifically and that the concern is the same in both cases and the one is bound up with the other. If we ponder that, we will comprehend that for setting up the diameters and eccentricities conjointly, there is need of more principles, outside of the five regular solids.
Fifthly [V]: To arrive at the movements between which the consonances have been set up, once more I impress upon the reader that in the Commentaries on Mars I have demonstrated from the sure observations of Brahe that daily arcs, which are equal in one and the same eccentric circle, are not traversed with equal speed; but that these differing delays in equal parts of the eccentric observe the ratio of their distances from the sun, the source of movement; and conversely, that if equal times are assumed, namely, one natural day in both cases, the corresponding true diurnal arcs [278] of one eccentric orbit have to one another the ratio which is the inverse of the ratio of the two distances from the sun. Moreover, I demonstrated at the same time that the planetary orbit is elliptical and the sun, the source of movement, is at one of the foci of this ellipse; and so, when the planet has completed a quarter of its total circuit from its aphelion, then it is exactly at its mean distance from the sun, midway between its greatest distance at the aphelion and its least at the perihelion. But from these two axioms it results that the diurnal mean movement of the planet in its eccentric is the same as the true diurnal arc of its eccentric at those moments wherein the planet is at the end of the quadrant of the eccentric measured from the aphelion, although that true quadrant appears still smaller than the just quadrant. Furthermore, it follows that the sum of any two true diurnal eccentric arcs, one of which is at the same distance from the aphelion that the other is from the perihelion, is equal to the sum of the two mean diurnal arcs. And as a consequence, since the ratio of circles is the same as that of the diameters, the ratio of one mean diurnal arc to the sum of all the mean and equal arcs in the total circuit is the same as the ratio of the mean diurnal arc to the sum of all the true eccentric arcs, which are the same in number but unequal to one another. And those things should first be known concerning the true diurnal arcs of the eccentric and the true movements, so that by means of them we may understand the movements which would be apparent if we were to suppose an eye at the sun.
Sixthly [VI]: But as regards the arcs which are apparent, as it were, from the sun, it is known even from the ancient astronomy that, among true movements which are equal to one another, that movement which is farther distant from the centre of the world (as being at the aphelion) will appear smaller to a beholder at that centre, but the movement which is nearer (as being at the perihelion) will similarly appear greater. Therefore, since moreover the true diurnal arcs at the near distance are still greater, on account of the faster movement, and still smaller at the distant aphelion, on account of the slowness of the movement, I demonstrated in the Commentaries on Mars that the ratio of the apparent diurnal arcs of one eccentric circle is fairly exactly the inverse ratio of the squares of their distances from the sun. For example, if the planet one day when it is at
a distance from the sun of 10 parts, in any measure whatsoever, but on the opposite day, when it is at the perihelion, of 9 similar parts: it is certain that from the sun its apparent progress at the aphelion will be to its apparent progress at the perihelion, as 81 : 100.
But that is true with these provisos: First, that the eccentric arcs should not be great, lest they partake of distinct distances which are very different—i.e., lest the distances of their termini from the apsides cause a perceptible variation; second, that the eccentricity should not be very great, for the greater its eccentricity (viz., the greater the arc becomes) the more the angle of its apparent movement increases beyond the measure of its approach to the sun, by Theorem 8 of Euclid's Optics; none the less in small arcs even a great distance is of no moment, as I have remarked in my Optics, Chapter 11. But there is another reason why I make that admonition. For the eccentric arcs around the mean anomalies are viewed obliquely from the centre of the sun. This obliquity subtracts from the magnitude of the apparent movement, since conversely the arcs around the apsides are presented directly to an eye stationed as it were at the sun. Therefore, when the eccentricity is very great, then the eccentricity takes away perceptibly from the ratio of the movements; if without any diminution we apply the mean diurnal movement to the mean distance, as if at the mean distance, it would appear to have the same magnitude which it does have—as will be apparent below in the case of Mercury. All these things are treated at greater length in Book V of the Epitome of Copernican Astronomy; but they have been mentioned here too because they have to do with the very terms of the celestial consonances, considered in themselves singly and separately.
Seventhly [VII]: If by chance anyone runs into those diurnal movements which are apparent [279] to those gazing not as it were from the sun but from the Earth, with which movements Book VI of the Epitome of Copernican Astronomy deals, he should know that their rationale is plainly not considered in this business. Nor should it be, since the Earth is not the source of the planetary movements, nor can it be, since with respect to deception of sight they degenerate not only into mere quiet or apparent stations but even into retrogradation, in which way a whole infinity of ratios is assigned to all the planets, simultaneously and equally. Therefore, in order that we may hold for certain what sort of ratios of their own are constituted by the single real eccentric orbits (although these too are still apparent, as it were to one looking from the sun, the source of movement), first we must remove from those movements of their own this image of the adventitious annual movement common to all five, whether it arises from the movement of the Earth itself, according to Copernicus, or from the annual movement of the total system, according to Tycho Brahe, and the winnowed movements proper to each planet are to be presented to sight.
Eighthly [viii]: So far we have dealt with the different delays or arcs of one and the same planet. Now we must also deal with the comparison of the movements of two planets. Here take note of the definitions of the terms which will be necessary for us. We give the name of nearest apsides of two planets to the perihelion of the upper and the aphelion of the lower, notwithstanding that they tend not towards the same region of the world but towards distinct and perhaps contrary regions. By extreme movements understand the slowest and the fastest of the whole planetary circuit; by converging or converse extreme movements, those which are at the nearest apsides of two planets—namely, at the
perihelion of the upper planet and the aphelion of the lower; by diverging or diverse, those at the opposite apsides—namely, the aphelion of the upper and the perihelion of the lower. Therefore again, a certain part of my Mysterium Cosmographicum, which was suspended twenty-two years ago, because it was not yet clear, is to be completed and herein inserted. For after finding the true intervals of the spheres by the observations of Tycho Brahe and continuous labour and much time, at last, at last the right ratio of the periodic times to the spheres
yet looked to him, and, after much time, came,
and, if you want the exact time, was conceived mentally on the 8th of March in this year One Thousand Six Hundred and Eighteen but unfelicitously submitted to calculation and rejected as false, finally, summoned back on the 15th of May, with a fresh assault undertaken, outfought the darkness of my mind by the great proof afforded by my labor of seventeen years on Brahe's observations and meditation upon it uniting in one concord, in such fashion that I first believed I was dreaming and was presupposing the object of my search among the principles. But it is absolutely certain and exact that the ratio which exists between the periodic times of any two planets is precisely the ratio of the 3/2th power of the mean distances, i.e., of the spheres themselves; provided, however, that the arithmetic mean between both diameters of the elliptic orbit be slightly less than the longer diameter. And so if any one take the period, say, of the Earth, which is one year, and the period of Saturn, which is thirty years, and extract the cube roots of this ratio and then square the ensuing ratio by squaring the cube roots, he will have as his numerical products the most just ratio of the distances of the Earth and Saturn from the sun. 1 For the cube root of 1 is 1, and the square of it is 1; and the cube root of 30 is greater than 3, and therefore the square of it is greater than 9. And Saturn, at its mean distance from the sun, is slightly higher [280] than nine times the mean distance of the Earth from the sun. Further on, in Chapter 9, the use of this theorem will be necessary for the demonstration of the eccentricities.
Ninthly [IX]: If now you wish to measure with the same yardstick, so to speak, the true daily journeys of each planet through the ether, two ratios are to be compounded—the ratio of the true (not the apparent) diurnal arcs of the eccentric, and the ratio of the mean intervals of each planet from the sun (because that is the same as the ratio of the amplitude of the spheres), i.e., the true diurnal arc of each planet is to be multiplied by the semidiameter of its sphere: the products will be numbers fitted for investigating whether or not those journeys are in harmonic ratios.
Tenthly [X]: In order that you may truly know how great any one of these diurnal journeys appears to be to an eye stationed as it were at the sun, although this same thing can be got immediately from the astronomy, nevertheless it will also be manifest if you multiply the ratio of the journeys by the inverse ratio not of the mean, but of the true intervals which exist at any position on
the eccentrics: multiply the journey of the upper by the interval of the lower planet from the sun, and conversely multiply the journey of the lower by the interval of the upper from the sun.
Eleventhly [XI]: And in the same way, if the apparent movements are given, at the aphelion of the one and at the perihelion of the other, or conversely or alternately, the ratios of the distances of the aphelion of the one to the perihelion of the other may be elicited. But where the mean movements must be known first, viz., the inverse ratio of the periodic times, wherefrom the ratio of the spheres is elicited by Article VIII above: then if the mean proportional between the apparent movement of either one of its mean movement be taken, this mean proportional is to the semidiameter of its sphere (which is already known) as the mean movement is to the distance or interval sought. Let the periodic times of two planets be 27 and 8. Therefore the ratio of the mean diurnal movement of the one to the other is 8 : 27. Therefore the semidiameters of their spheres will be as 9 to 4. For the cube root of 27 is 3, that of 8 is 2, and the squares of these roots, 3 and 2, are 9 and 4. Now let the apparent aphelial movement of the one be 2 and the perihelial movement of the other 33⅓. The mean proportionals between the mean movements 8 and 27 and these apparent ones will be 4 and 30. Therefore if the mean proportional 4 gives the mean distance of 9 to the planet, then the mean movement of 8 gives an aphelial distance 18, which corresponds to the apparent movement 2; and if the other mean proportional 30 gives the other planet a mean distance of 4, then its mean movement of 27 will give it a perihelial interval of 3 3/5. I say, therefore, that the aphelial distance of the former is to the perihelial distance of the latter as 18 to 3 3/5. Hence it is clear that if the consonances between the extreme movements of two planets are found and the periodic times are established for both, the extreme and the mean distances are necessarily given, wherefore also the eccentricities.
Twelfthly [XII]: It is also possible, from the different extreme movements of one and the same planet, to find the mean movement. The mean movement is not exactly the arithmetic mean between the extreme movements, nor exactly the geometric mean, but it is as much less than the geometric mean as the geometric mean is less than the [arithmetic] mean between both means. Let the two extreme movements be 8 and 10: the mean movement will be less than 9, and also less than the square root of 80 by half the difference between 9 and the square root of 80. In this way, if the aphelial movement is 20 and the perihelial 24, the mean movement will be less than 22, even less than the square root of 480 by half the difference between that root and 22. There is use for this theorem in what follows.
[281] Thirteenthly [XIII]: From the foregoing the following proposition is demonstrated, which is going to be very necessary for us: Just as the ratio of the mean movements of two planets is the inverse ratio of the 3/2th powers of the spheres, so the ratio of two apparent converging extreme movements always falls short of the ratio of the 3/2th powers of the intervals corresponding to those extreme movements; and in what ratio the product of the two ratios of the corresponding intervals to the two mean intervals or to the semidiameters of the two spheres falls short of the ratio of the square roots of the spheres, in that ratio does the ratio of the two extreme converging movements exceed the ratio of the corresponding intervals; but if that compound ratio were to exceed the
ratio of the square roots of the spheres, then the ratio of the converging movements would be less than the ratio of their intervals. 1
Let the ratio of the spheres be DH : AE; let the ratio of the mean movements be HI : EM, the 3/2th power of the inverse of the former.
 Click to enlarge |
Let the least interval of the sphere of the first be CG; and the greatest interval of the sphere of the second be BF; and first let DH : CG comp. BF : AE be smaller than the ½th power of DH : AE. And let GH be the apparent perihelial movement of the upper planet, and FL the aphelial of the lower, so that they are converging extreme movements.
I say that
BF3/2 : CG3/2.
For
and
Hence
But
by a fixed ratio of defect, as was assumed. Therefore too
AE : DH
by a ratio of defect which is the square of the former. But by number VIII
Therefore let the ratio which is smaller by the total square of the ratio of defect be divided into the ratio of the 3/2th powers; that is,
by the excess squared. But
Therefore
by the excess squared. But
And
by the simple defect. Therefore
by the simple excess. But
but by the excess squared. But the excess squared is greater than the simple excess. Therefore the ratio of the movements GK to FL is greater than the ratio of the corresponding intervals BF to CG.
In fully the same way, it is demonstrated even contrariwise that if the planets approach one another in G and F beyond the mean distances in H and E, in such fashion that the ratio of the mean distances DH : AE becomes less than DH½ : AE½, then the ratio of the movements GK : FL becomes less than the ratio of the corresponding intervals BF: CG. For you need to do nothing more than to change the words greater to less, > to <, excess to defect, and conversely.
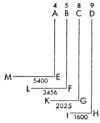
In suitable numbers, because the square root of 4/9 is 2/3; and 5/8 is even greater than 2/3 by the ratio of excess 15/16; and the square of the ratio 8 : 9 [282] is the ratio 1600 : 2025, i.e., 64 : 81; and the square of the ratio 4 : 5 is the ratio 3456 : 5400, i.e., 16 : 25; and finally the 3/2th power of the ratio 4 : 9 is the ratio 1600 : 5400, i.e., 8 : 27: therefore too the ratio 2025 : 3456, i.e., 75 : 128, is even greater than 5 : 8, i.e., 75 : 120, by the same ratio of excess (i.e., 120 : 128), 15 : 16; whence 2025 : 3456, the ratio of the converging movements, exceeds 5 : 8, the inverse ratio of the corresponding intervals, by as much as 5 : 8 exceeds 2 : 3, the square root of the ratio of the spheres. Or, what amounts to the same thing, the ratio of the two converging intervals is a mean between the ratio of the square roots of the spheres and the inverse ratio of the corresponding movements.
Moreover, from this you may understand that the ratio of the diverging movements is much greater than the ratio of the 3/2th powers of the spheres, since the ratio of the 3/2th powers is compounded with the squares of the ratio of the aphelial interval to the mean interval, and that of the mean to the perihelial.
Footnotes
1020:1 For in the Commentaries on Mars, chapter 48, page 232, I have proved that this Arithmetic mean is either the diameter of the circle which is equal in length to the elliptic orbit, or else is very slightly less.
1022:1 Kepler always measures the magnitude of a ratio from the greater term to the smaller, rather than from the antecedent to the consequent, as we do today. For example, as Kepler speaks, 2 : 3 is the same as 3 : 2, and 3 : 4 is greater than 7 : 8.—C. G. Wallis.
4. IN WHAT THINGS HAVING TO DO WITH THE PLANETARY MOVEMENTS HAVE THE HARMONIC CONSONANCES BEEN EXPRESSED BY THE CREATOR, AND IN WHAT WAY?
Accordingly, if the image of the retrogradation and stations is taken away and the proper movements of the planets in their real eccentric orbits are winnowed out, the following distinct things still remain in the planets: 1) The distances from the sun. 2) The periodic times. 3) The diurnal eccentric arcs. 4) The diurnal delays in those arcs. 5) The angles at the sun, and the diurnal arcs apparent to those as it were gazing from the sun. And again, all of these things, with the exception of the periodic times, are variable in the total circuit, most variable at the mean longitudes, but least at the extremes, when, turning away from one extreme longitude, they begin to return to the opposite. Hence when the planet is lowest and nearest to the sun and thereby delays the least in one degree of its eccentric, and conversely in one day traverses the greatest diurnal arc of its eccentric and appears fastest from the sun: then its movement remains for some time in this strength without perceptible variation, until, after passing the perihelion, the planet gradually begins to depart farther from the sun in a straight line; at that same time it delays longer in the degrees of its eccentric circle; or, if you consider the movement of one day, on the following day it goes forward less and appears even more slow from the sun until it has drawn close to the highest apsis and made its distance from the sun very great: for then longest of all does it delay in one degree of its eccentric; or on the contrary in one day it traverses its least arc and makes a much smaller apparent movement and the least of its total circuit.
Finally, all these things may be considered either as they exist in any one planet at different times or as they exist in different planets: whence, by the assumption of an infinite amount of time, all the affects of the circuit of one planet can concur in the same moment of time with all the affects of the circuit of another planet and be compared, and then the total eccentrics, as compared with one another, have the same ratio as their semidiameters or mean intervals; but the arcs of two eccentrics, which are similar or designated by the same number [of degrees], nevertheless have their true lengths unequal in the ratio of their eccentrics. For example, one degree in the sphere of Saturn is approximately twice as long as one degree in the sphere of Jupiter. And conversely, the diurnal arcs of the eccentrics, as expressed in astronomical terms, do not exhibit the ratio of the true journeys which the globes complete in one day [283] through the ether, because the single units in the wider circle of the upper planet denote a quarter part of the journey, but in the narrower circle of the lower planet a smaller part.
Therefore let us take the second of the things which we have posited, namely, the periodic times of the planets, which comprehend the sums made up of all the delays—long, middling, short—in all the degrees of the total circuit. And we found that from antiquity down to us, the planets complete their periodic returns around the sun, as follows in the table:
Accordingly, in these periodic times there are no harmonic ratios, as is easily apparent, if the greater periods are continuously halved, and the smaller are continuously doubled, so that, by neglecting the intervals of an octave, we can investigate the intervals which exist within one octave.
All the last numbers, as you see, are counter to harmonic ratios and seem, as it were, irrational. For let 687, the number of days of Mars, receive as its measure 120, which is the number of the division of the chord: according to this measure Saturn will have 117 for one sixteenth of its period, Jupiter less than 95 for one eighth of its period, the earth less than 64, Venus more than 78 for twice its period, Mercury more than 61 for four times its period. These numbers do not
make any harmonic ratio with 120, but their neighbouring numbers—60, 75, 80, and 96—do. And so, whereof Saturn has 120, Jupiter has approximately 97, the Earth more than 65, Venus more than 80, and Mercury less than 63. And whereof Jupiter has 120, the Earth has less than 81, Venus less than 100, Mercury less than 78. Likewise, whereof Venus has 120, the Earth has less than 98, Mercury more than 94. Finally, whereof the Earth has 120, Mercury has less than 116. But if the free choice of ratios had been effective here, consonances which are altogether perfect but not augmented or diminished would have been taken. Accordingly we find that God the Creator did not wish to introduce harmonic ratios between the sums of the delays added together to form the periodic times.
[284] And although it is a very probable conjecture (as relying on geometrical demonstrations and the doctrine concerning the causes of the planetary movements given in the Commentaries on Mars) that the bulks of the planetary bodies are in the ratio of the periodic times, so that the globe of Saturn is about thirty times greater than the globe of the Earth, Jupiter twelve times, Mars less than two, the Earth one and a half times greater than the globe of Venus and four times greater than the globe of Mercury: not therefore will even these ratios of bodies be harmonic.
But since God has established nothing without geometrical beauty, which was not bound by some other prior law of necessity, we easily infer that the periodic times have got their due lengths, and thereby the mobile bodies too have got their bulks, from something which is prior in the archetype, in order to express which thing these bulks and periods have been fashioned to this measure, as they seem disproportionate. But I have said that the periods are added up from the longest, the middling, and the slowest delays: accordingly geometrical fitnesses must be found either in these delays or in anything which may be prior to them in the mind of the Artisan. But the ratios of the delays are bound up with the ratios of the diurnal arcs, because the arcs have the inverse ratio of the delays. Again, we have said that the ratios of the delays and intervals of any one planet are the same. Then, as regards the single planets, there will be one and the same consideration of the following three: the arcs, the delays in equal arcs, and the distance of the arcs from the sun or the intervals. And because all these things are variable in the planets, there can be no doubt but that, if these things were allotted any geometrical beauty, then, by the sure design of the highest Artisan, they would have been received that at their extremes, at the aphelial and perihelial intervals, not at the mean intervals lying in between. For, given the ratios of the extreme intervals, there is no need of a plan to fit the intermediate ratios to a definite number. For they follow of themselves, by the necessity of planetary movement, from one extreme through all the intermediates to the other extreme.
Therefore the intervals are as follows, according to the very accurate observations of Tycho Brahe, by the method given in the Commentaries on Mars and investigated in very persevering study for seventeen years.
Intervals Compared with Harmonic Ratios 1
[285] Therefore the extreme intervals of no one planet come near consonances except those of Mars and Mercury.
But if you compare the extreme intervals of different planets with one another, some harmonic light begins to shine. For the extreme diverging intervals of Saturn and Jupiter make slightly more than the octave; and the converging,
a mean between the major and minor sixths. So the diverging extremes of Jupiter and Mars embrace approximately the double octave; and the converging, approximately the fifth and the octave. But the diverging extremes of the Earth and Mars embrace somewhat more than the major sixth; the converging, an augmented fourth. In the next couple, the Earth and Venus, there is again the same augmented fourth between the converging extremes; but we lack any harmonic ratio between the diverging extremes: for it is less than the semi-octave (so to speak) i.e., less than the square root of the ratio 2 : 1. Finally, between the diverging extremes of Venus and Mercury there is a ratio slightly
less than the octave compounded with the minor third; between the converging there is a slightly augmented fifth.
Accordingly, although one interval was somewhat removed from harmonic ratios, this success was an invitation to advance further. Now my reasonings were as follows: First, in so far as these intervals are lengths without movement, they are not fittingly examined for harmonic ratios, because movement is more properly the subject of consonances, by reason of speed and slowness. Second, inasmuch as these same intervals are the diameters of the spheres, it is believable that the ratio of the five regular solids applied proportionally is more dominant in them, because the ratio of the geometrical solid bodies to the celestial spheres (which are everywhere either encompassed by celestial matter, as the ancients hold, or to be encompassed successively by the accumulation of many revolutions) is the same as the ratio of the plane figures which may be inscribed in a circle (these figures engender the consonances) to the celestial circles of movements and the other regions wherein the movements take place. Therefore, if we are looking for consonances, we should look for them not in these
intervals in so far as they are the semidiameters of spheres but in them in so far as they are the measures of the movements, i.e., in the movements themselves, rather. Absolutely no other than the mean intervals can be taken as the semi-diameters of the spheres; but we are here dealing with the extreme intervals. Accordingly, we are not dealing with the intervals in respect to their spheres but in respect to their movements.
Accordingly, although for these reasons I had passed on to the comparison of the extreme movements, at first the ratios of the movements remained the same in magnitude as those which were previously the ratios of the intervals, only inverted. Wherefore too, certain ratios, which are discordant and foreign to harmonies, as before, have been found between the movements. But once again I judged that this happened to me deservedly, because I compared with one another eccentric arcs which are not expressed and numbered by a measure of the same magnitude but are numbered in degrees and minutes which are of diverse magnitude in diverse planets, nor do they from our place give the appearance of being as great as the number of each says, except only at the centre of the eccentric of each planet, which centre rests upon no body; and hence it is also unbelievable that there is any sense or natural instinct in that place in the world which is capable of perceiving this; or, rather, it was impossible, if I was comparing the eccentric arcs of different planets with respect to their appearance at their centres, which are different for different planets. But if diverse apparent magnitudes are compared with one another, they ought to be apparent in one place in the world in such a way that that which possesses the faculty of comparing them may be present in that place from which they are all apparent. Accordingly, I judged that the appearance of these eccentric arcs should be removed from the mind or else should be formed differently. But if I removed the appearance and applied my mind to the diurnal journeys of the planets, I saw that I had to employ the rule which I gave in Article IX of the preceding chapter.
[286] Accordingly if the diurnal arcs of the eccentric are multiplied by the mean intervals of the spheres, the following journeys are produced:
Thus Saturn traverses barely one seventh of the journey of Mercury; and hence, as Aristotle judged consonant with reason in Book II of On the Heavens, the planet which is nearer the sun always traverses a greater space than the planet which is farther away—as cannot hold in the ancient astronomy.
And indeed, if we weigh the thing fairly carefully, it will appear to be not very probable that the most wise Creator should have established harmonies between the planetary journeys in especial. For if the ratios of the journeys are harmonic, all the other affects which the planets have will be necessitated and bound up with the journeys, so that there is no room elsewhere for establishing harmonies. But whose good will it be to have harmonies between the journeys, or who will perceive these harmonies? For there are two things which disclose to us harmonies in natural things: either light or sound: light apprehended through the eyes or hidden senses proportioned to the eyes, and sound through the ears. The mind seizes upon these forms and, whether by instinct (on which Book IV speaks profusely) or by astronomical or harmonic ratiocination, discerns the concordant from the discordant. Now there are no sounds in the heavens, nor is the movement so turbulent that any noise is made by the rubbing against the ether. Light remains. If light has to teach these things about the planetary journeys, it will teach either the eyes or a sensorium analogous to the eyes and situated in a definite place; and it seems that sense-perception must be present there in order that light of itself may immediately teach. Therefore there will be sense-perception in the total world, namely in order that the movements of all the planets may be presented to sense-perceptions at the same time. For that former route—from observations through the longest detours of geometry and arithmetic, through the ratios of the spheres and the other things which must be learned first, down to the journeys which have been exhibited—is too long for any natural instinct, for the sake of moving which it seems reasonable that the harmonies have been introduced.
Therefore with everything reduced to one view, I concluded rightly [287] that the true journeys of the planets through the ether should be dismissed, and that we should turn our eyes to the apparent diurnal arcs, according as they are all apparent from one definite and marked place in the world—namely, from the solar body itself, the source of movement of all the planets; and we must see, not how far away from the sun any one of the planets is, nor how much space it traverses in one day (for that is something for ratiocination and astronomy, not for instinct), but how great an angle the diurnal movement of each planet subtends in the solar body, or how great an arc it seems to traverse in one common circle described around the sun, such as the ecliptic, in order that these appearances, which were conveyed to the solar body by virtue of light, may be able to flow, together with the light, in a straight line into creatures, which are partakers of this instinct, as in Book IV we said the figure of the heavens flowed into the foetus by virtue of the rays.
Therefore, if you remove from the proper planetary movement the parallaxes of the annual orbit, which gives them the mere appearances of stations and retrogradations, Tycho's astronomy teaches that the diurnal movements of the planets in their orbits (which are apparent as it were to spectator at the sun) are as shown in the table on the opposite page.
Note that the great eccentricity of Mercury makes the ratio of the movements differ somewhat from the ratio of the square of the distances. For if you make the square of the ratio of 100, the mean distance, to 121, the aphelial distance, be the ratio of the aphelial movement to the mean movement of 245´32″, then an aphelial movement of 167 will be produced; and if the square of the ratio of 100 to 79, the perihelial distance, be the ratio of the perihelial to the same mean movement, then the perihelial movement will become 393; and both cases are
greater than I have here laid down, because the mean movement at the mean anomaly, viewed very obliquely, does not appear as great, viz., not as great as
245'32", but about 5' less. Therefore, too, lesser aphelial and perihelial movements will be elicited. But the aphelial [appears] lesser and the perihelial greater, on account of theorem 8, Euclid's Optics, as I remarked in the preceding Chapter, Article VI.
Accordingly, I could mentally presume, even from the ratios of the diurnal eccentric arcs given above, that there were harmonies and concordant intervals between these extreme apparent movements of the single planets, since I saw that everywhere there the square roots of harmonic ratios were dominant, but knew that the ratio of the apparent movements was the square of the ratio of the eccentric movements. But it is possible by experience itself, or without any ratiocination to prove what is affirmed, as you see [288] in the preceding table. The ratios of the apparent movements of the single planets approach very close to harmonies, in such fashion that Saturn and Jupiter embrace slightly more than the major and minor thirds, Saturn with a ratio of excess of 53 : 54, and Jupiter with one of 54 : 55 or less, namely approximately a sesquicomma; the Earth, slightly more (namely 137 : 138, or barely a semicomma) than a semitone; Mars somewhat less (namely 29 : 30, which approaches 34 : 35 or 35 : 36) than a fifth; Mercury exceeds the octave by a minor third rather than a whole tone, viz., it is about 38 : 39 (which is about two commas, viz., 34 : 35 or 35 : 36) less than a whole tone. Venus alone falls short of any of the concords the diesis; for its ratio is between two and three commas, and it exceeds two thirds of a diesis, and is about 34 : 35 or 35 : 36, a diesis diminished by a comma.
The moon, too, comes into this consideration. For we find that its hourly apogeal movement in the quadratures, viz., the slowest of all its movements, to be 26´26″; its perigeal movement in the syzygies, viz., the fastest of all, 35´12″, in which way the perfect fourth is formed very precisely. For one third of 26´26″ is 8´49″, the quadruple of which is 35´16″. And note that the consonance of the perfect fourth is found nowhere else between the apparent movements; note also the analogy between the fourth in consonances and the quarter in the phases. And so the above things are found in the movements of the single planets.
But in the extreme movements of two planets compared with one another, the radiant sun of celestial harmonies immediately shines at first glance, whether you compare the diverging extreme movements or the converging. For the ratio between the diverging movements of Saturn and Jupiter is exactly the duple or octave; that between the diverging, slightly more than triple or the octave and the fifth. For one third of 5´30″ is 1´50″, although Saturn has 1´46″ instead of that. Accordingly, the planetary movements will differ from a consonance by a diesis more or less, viz., 26 : 27 or 27 : 28; and with less than one second acceding at Saturn's aphelion, the excess will be 34 : 35, as great as the ratio of the extreme movements of Venus. The diverging and converging movements of Jupiter and Mars are under the sway of the triple octave and the double octave and a third, but not perfectly. For one eighth of 38´1″ is 4´45″, although Jupiter has 4´30″; and between these numbers there is still a difference of 18 : 19, which is a mean between the semitone of 15 : 16 and the diesis of 24 : 25, namely, approximately a perfect lemma of 128 : 135. 1 Thus one fifth of 26´14″ is 5´15″, although Jupiter has 5´30″; accordingly in this case the quintuple ratio is diminished in the ratio of 21 : 22, the augment in the case of the other ratio, viz., approximately a diesis of 24 : 25.
The consonance 5 : 24 comes nearer, which compounds a minor instead of a major third with the double octave. For one fifth of 5´30″ is 1´6″, which if multiplied by 24 makes 26´24″, does not differ by more than a semicomma. Mars and the Earth have been allotted the least ratio, exactly the sesquialteral or perfect fifth: for one third of 57´3″ is 19´1″, the double of which is 38´2″, which is Mars’ very number, viz., 38´11″. They have also been allotted the greater ratio of 5 : 12, the octave and minor third, but more imperfectly. For one twelfth of 61´18″ is 5´6½″, which if multiplied by 5 gives 25´33″, although instead of that Mars has 26´14″. Accordingly, there is a deficiency of a diminished diesis approximately, viz., 35 : 36. But the Earth and Venus together have been allotted 3 : 5 as their greatest consonance and 5 : 8 as their least, the major and minor sixths, but again not perfectly. For one fifth of 97´37″, which if multiplied by 3 gives 58´33″, which is greater than the movement of the Earth in the ratio 34 : 35, which is approximately 35 : 36: by so much do the planetary ratios differ from the harmonic. Thus one eighth of 94´50″ is 11´51″ +, five times which is 59´16″, which is approximately equal to the mean movement of the Earth. Wherefore here the planetary ratio is less than the harmonic [289] in the ratio of 29 : 30 or 30 : 31, which is again approximately 35 : 36, the diminished diesis; and thereby this least ratio of these planets approaches the consonance of the perfect fifth. For one third of 94´50″ is 31´37″, the double of which is 63´14″, of which the 61´18″ of the perihelial movement of the Earth falls short in the ratio
of 31 : 32, so that the planetary ratio is exactly a mean between the neighbouring harmonic ratios. Finally, Venus and Mercury have been allotted the double octave as their greatest ratio and the major sixth as their least, but not absolute-perfectly. For one fourth of 384´ is 96´0″, although Venus has 94´50″. Therefore the quadruple adds approximately one comma. Thus one fifth of 164´ is 32´48″, which if multiplied by 3 gives 98´24″, although Venus has 97´37″. Therefore the planetary ratio is diminished by about two thirds of a comma, i.e., 126 : 127.
Accordingly the above consonances have been ascribed to the planets; nor is there any ratio from among the principal comparisons (viz., of the converging and diverging extreme movements) which does not approach so nearly to some consonance that, if strings were tuned in that ratio, the ears would not easily discern their imperfection--with the exception of that one excess between Jupiter and Mars.
Moreover, it follows that we shall not stray far away from consonances if we compare the movements of the same field. For if Saturn's 4 : 5 comp. 53 : 54 are compounded with the intermediate 1 : 2, the product is 2 : 5 comp. 53 : 54, which exists between the aphelial movements of Saturn and Jupiter. Compound with that Jupiter's 5 : 6 comp. 54 : 55, and the product is 5 : 12 comp 54 : 55, which exist between the perihelial movements of Saturn and Jupiter. Thus compound Jupiter's 5 : 6 comp. 54 : 55 with the intermediate ensuing ratio of 5 : 24 comp. 158 : 157, the product will be 1 : 6 comp. 36 : 35 between the aphelial movements. Compound the same 5 : 24 comp. 158 : 157 with Mars’ 2 : 3 comp. 30 : 29, and the product will be 5 : 36 comp. 25 : 24 approximately, i.e., 125 : 864 or about 1 : 7, between the perihelial movements. This ratio is still alone discordant. With 2 : 3 the third ratio among the intermediates, compound Mars’ 2 : 3 less 29 : 30; the result will be 4 : 9 comp. 30:29, i.e., 40 : 87, another discord between the aphelial movements. If instead of Mars’ you compound the Earth's 15 : 16 comp. 137 : 138, you will make 5 : 8 comp. 137 : 138 between the perihelial movements. And if with the fourth of the intermediates, 5 : 8 comp. 31 : 30, or 2 : 3 comp. 31 : 32, you compound the Earth's 15 : 16 comp. 137 : 138, the product will be approximately 3 : 5 between the aphelial movements of the Earth and Venus. For one fifth of 94´50″ is 18´58″, the triple of which is 56´54″, although the Earth has 57´3″. If you compound Venus’ 34 : 35 with the same ratio, the result will be 5 : 8 between the perihelial movements. For one eighth of 97´37″ is 12´12″+ which if multiplied by 5 gives 61´1″, although the Earth has 61´18″. Finally, if with the last of the intermediate ratios, 3 : 5 comp. 126 : 127 you compound Venus’ 34 : 35, the result is 3 : 5 comp. 24 : 25, and the interval, compounded of both, between the aphelial movements, is dissonant. But if you compound Mercury's 5 : 12 comp. 38 : 39, the double octave or 1 : 4 will be diminished by approximately a whole diesis, in proportion to the perihelial movements.
Accordingly, perfect consonances are found: between the converging movements of Saturn and Jupiter, the octave; between the converging movements of Jupiter and Mars, the octave and minor third approximately; between the converging movements of Mars and the Earth, the fifth; between their perihelial, the minor sixth; between the extreme converging movements of Venus and Mercury, the major sixth; between the diverging or even between the perihelial, the double octave: whence without any loss to an astronomy which has been built, most subtly of all, upon Brahe's observations, it seems that the residual very slight
discrepancy can be discounted, especially in the movements of Venus and Mercury.
But you will note that where there is no perfect major consonance, as between Jupiter and Mars, there alone have I found the placing of the solid figure to be approximately perfect, since the perihelial distance of Jupiter is approximately three times the aphelial distance of Mars, in such fashion that this pair of planets strives after the perfect consonance in the intervals which it does not have in the movements.
[290] You will note, furthermore, that the major planetary ratio of Saturn
and Jupiter exceeds the harmonic, viz., the triple, by approximately the same quantity as belongs to Venus; and the common major ratio of the converging and diverging movements of Mars and the Earth are diminished by approximately the same. You will note thirdly that, roughly speaking, in the upper planets the consonances are established between the converging movements, but in the lower planets, between movements in the same field. And note fourthly that between the aphelial movements of Saturn and the Earth there are approximately five octaves; for one thirty-second of 57´3″ is 1´47″, although the aphelial movement of Saturn is 1´46″.
Furthermore, a great distinction exists between the consonances of the single planets which have been unfolded and the consonances of the planets in pairs. For the former cannot exist at the same moment of time, while the latter absolutely can; because the same planet, moving at its aphelion, cannot be at the same time at the opposite perihelion too, but of two planets one can be at its aphelion and the other at its perihelion at the same moment of time. And so the ratio of plain-song or monody, which we call choral music and which alone was known to the ancients, 1 to polyphony—called "figured song,"; 2 the invention of the latest generations—is the same as the ratio of the consonances which the single planets designate to the consonances of the planets taken together. And so, further on, in Chapters 5 and 6, the single planets will be compared to the choral music of the ancients and its properties will be exhibited in the planetary movements. But in the following chapters, the planets taken together and the figured modern music will be shown to do similar things.
Footnotes
1026:1 GENERAL NOTE: Throughout this text Kepler's concinna and inconcinna are translated as "concordant" and "discordant." Concinna is usually used by Kepler of all intervals whose ratios occur within the "natural system" or the just intonation of the scale. Inconcinna refers to all ratios that lie outside of this system of tuning. "Consonant" (consonans) and "dissonant" (dissonans) refer to qualities which can be applied to intervals within the musical system, in other words to "concords." "Harmony" (harmonia) is used sometimes in the sense of "concordance" and sometimes in the sense of "consonance."
Genus durum and genus molle are translated either as "major mode" and "minor mode," or as "major scale" and "minor scale," or as "major kind" and "minor kind" (of consonances). The use of modus, to refer to the ecclesiastical modes, occurs only in Chapter 6.
As our present musical terms do not apply strictly to the music of the sixteenth and seventeenth centuries, a brief explanation of terms here may be useful. This material is taken from Kepler's Harmonies of the World, Book III.
An octave system in the minor scale (Systema octavae in cantu molli)
In the major scale (In cantu duro)
As in all music, these scales can be repeated at one or more octaves above. The ratios would then all be halved, i.e.,
Various intervals which Kepler considers are:
All these are simple intervals. When one or more octaves are added to any simple intervals the resultant interval is a "compound" interval.
1 : 3 equals ½ × ⅔—an octave and a perfect fifth
3 : 32 equals (½)3 × ¾—three octaves and a perfect fourth
1 : 20 equals (½)4 × (16/20)—four octaves and a major third
Concords: All intervals from diesis downward on above list.
Consonances: Minor and major thirds and sixths, perfect fourth, fifth, and octave.
"Adulterine" consonances: sub-minor third, ditone, lesser imperfect fourth and fifth, greater imperfect fourth and fifth, imperfect minor sixth, greater major sixth.
Dissonances: All other intervals.
Throughout this work Kepler, after the fashion of the theorists of his time, uses the ratios of string lengths rather than the ratios of vibrations as is usually done today. String lengths are, of course, inversely proportionate to the vibrations. That is, string lengths 4 : 5 are expressed in vibrations as 5 :4. This accounts for the descending order of the scale, which follows the increasing numerical order. It is an interesting fact that Kepler's minor and major scales are inversions of each other and hence, when expressed in ratios of vibrations, are in the opposite order from those in ratios of string lengths:
An arbitrary pitch G is chosen to situate these ratios. This g or "gamma" was usually the lowest tone of the sixteenth-century musical gamut.
ELLIOTT CARTER, JR.
1032:1 cf. Footnote to Intervals Compared with Harmonic Ratios, p. 1026.
1034:1 The choral music of the Greeks was monolinear, everyone singing the same melody together.—E. C., Jr.
1034:2 In plain-song all the time values of the notes were approximately equal, while in "figured song" time values of different lengths were indicated by the notes, which gave composers an opportunity both to regulate the way different contrapuntal parts joined together and to produce many expressive effects. Practically all melodies since this time are in "figured song" style.—E. C., Jr.
5. IN THE RATIOS OF THE PLANETARY MOVEMENTS WHICH ARE APPARENT AS IT WERE TO SPECTATORS AT THE SUN, HAVE BEEN EXPRESSED THE PITCHES OF THE SYSTEM, OR NOTES OF THE MUSICAL SCALE, AND THE MODES OF SONG [GENERA CANTUS], THE MAJOR AND THE MINOR 3
Therefore by now I have proved by means of numbers gotten on one side from astronomy and on the other side from harmonics that, taken in every which way, harmonic ratios hold between these twelve termini or movements of the six planets revolving around the sun or that they approximate such ratios within an imperceptible part of least concord. But just as in Book III in the first chapter, we first built up the single harmonic consonances separately, and then
we joined together all the consonances—as many as there were—in one common system or musical scale, or, rather, in one octave of them which embraces the rest in power, and by means of them we separated the others into their degrees or pitches [loca] and we did this in such a way that there would be a scale; so now also, after the discovery of the consonances [harmoniis] which God Himself has embodied in the world, we must consequently see whether those single consonances stand so separate that they have no kinship with the rest, or whether all are in concord with one another. Notwithstanding it is easy to conclude, without any further inquiry, that those consonances were fitted together by the highest prudence in such fashion that they move one another about within one frame, so to speak, and do not jolt one another out of it; since indeed we see that in such a manifold comparison of the same terms there is no place where consonances do not occur. For unless in one scale all the consonances were fitted to all, it could easily have come about (and it has come about wherever necessity thus urges it) that many dissonances should exist. For example, if someone had set up a major sixth between the first and the second term, and likewise a major third between the second and the third term, without taking the first into account, then he would admit a dissonance and the discordant interval 12 : 25 between the first and third.
But come now, let us see whether that which we have already inferred by reasoning is really found in this way. [291] But let me premise some cautions, that we may be the less impeded in our progress. First, for the present, we must conceal those augments or diminutions which are less than a semitone; for we shall see later on what causes they have. Second, by continuous doubling or contrary halving of the movements, we shall bring everything within the range of one octave, on account of the sameness of consonance in all the octaves.
Accordingly the numbers wherein all the pitches or clefs [loca seu claves] of the octave system are expressed have been set out in a table in Book III, Chapter 7 1,
i.e., understand these numbers of the length of two strings. As a consequence, the speeds of the movements will be in the inverse ratios.
Now let the planetary movements be compared in terms of parts continuously halved. Therefore
Now the aphelial movement of Saturn at its slowest—i.e., the slowest movement—marks G, the lowest pitch in the system with the number 1´46″. Therefore the aphelial movement of the Earth will mark the same pitch, but five octaves higher, because its number is 1´47″, and who wants to quarrel about one second in the aphelial movement of Saturn? But let us take it into account, nevertheless; the difference will not be greater than 106 : 107, which is less than a comma. If you add 27″, one quarter of this 1´47″, the sum will be 2´14″, although the perihelial movement of Saturn has 2´15″; similarly the aphelial movement of Jupiter, but one octave higher. Accordingly, these two movements mark the note b, or else are very slightly higher. Take 36″, one third of 1´47″, and add it to the whole; you will get as a sum 2´23″ for the note c; and here's the perihelion of Mars of the same magnitude but four octaves higher. To this same 1´47″ add also 54″, half of it, and the sum will be 2´41″ for the note d; and here the perihelion of Jupiter is at hand, but one octave higher, for it occupies the nearest number, viz., 2´45″. If you add two thirds, viz., 1´11″, the sum will be 2´58″; and here's the aphelion of Venus at 2´58″. Accordingly, it will mark the pitch or the note e, but five octaves higher. And the perihelial movement of Mercury, which is 3´0″, does not exceed it by much but is seven octaves higher. Finally, divide the double of 1´47″, viz., 3´34″, into nine parts and subtract one part of 24″ from the whole; 3´10″ will be left for the note f, which the 3´17″ of the aphelial movement of Mars marks approximately but three octaves higher; and this number is slightly greater than the just number and approaches the note f sharp. For if one sixteenth of 3´34″, viz., 13½″, is subtracted from 3´34″, then 3´20½″ is left, to which 3´17″ is very near. And indeed in music f sharp is often employed in place of f, as we can see everywhere.
Accordingly all the notes of the major scale [cantus duri] (except the note a which was not marked by harmonic division, in Book III, Chapter 2) are marked by all the extreme movements of the planets, except the perihelial movements of Venus and the Earth [292] and the aphelial movement of Mercury, whose number, 2´34″, approaches the note c sharp. For subtract from the 2´41″ of d one sixteenth or 10″, and 2´30″ remains for the note c sharp. Thus only the perihelial movement of Venus and the Earth are missing from this scale, as you may see in the table.
On the other hand, if the beginning of the scale is made at 2´15″, the aphelial movement of Saturn, and we must express the note G in those degrees: then for the note A is 2´32″, which closely approaches the aphelial movement of Mercury; for the note b flat, 2´42″, which is approximately the perihelial movement of Jupiter, by the equipollence of octaves; for the note c, 3´0″, approximately the perihelial movement of Mercury and Venus; for the note d, 3´23″ and the aphelial movement of Mars is not much graver, viz., 3´17″, so that here the number is about as much less than its note as previously the same number was greater than its note; for the note e flat, 3´36″, which the aphelial movement of the Earth approximates; for the note e, 3´50″, and the perihelial movement of the Earth is 3´49″; but the aphelial movement of Jupiter again occupies g. In this way, all the notes except f are expressed within one octave of the minor scale by most of the aphelial and perihelial movements of the planets, especially by those which were previously omitted, as you see in the table.
Previously, however, f sharp was marked and a omitted; now a is marked, f sharp is omitted; for the harmonic division in Chapter 2 also omitted the note f.
Accordingly, the musical scale or system of one octave with all its pitches, by means of which natural song 1 is transposed in music, has been expressed in the heavens by a twofold way and in two as it were modes of song. There is this sole difference: in our harmonic sectionings both ways start together from one and the same terminus G; but here, in the planetary movements, that which was previously b now becomes G in the minor mode.
For as in music 2160 : 1800, or 6 : 5, so in that system which the heavens express, 1728 : 1440, namely, also 6 : 5; and so for most of the remaining, 2160 : 1800, 1620, 1440, 1350, 1080 as 1728 : 1440, 1296, 1152, 1080, 864.
Accordingly you won't wonder any more that a very excellent order of sounds or pitches in a musical system or scale has been set up by men, since you see that they are doing nothing else in this business except to play the apes of God the Creator and to act out, as it were, a certain drama of the ordination of the celestial movements.
But there still remains another way whereby we may understand the twofold musical scale in the heavens, where one and the same system but a twofold tuning [tensio] is embraced, one at the aphelial movement of Venus, the other at the perihelial, because the variety of movements of this planet is of the least magnitude, as being such as is comprehended within the magnitude of the diesis, the least concord. And the aphelial tuning [tensio], as above, has been given to the aphelial movements of Saturn, the Earth, Venus, and (relatively speaking) Jupiter, in G, e, b, but to the perihelial movements of Mars and (relatively speaking) Saturn and, as is apparent at first glance, to those of Mercury, in c, e, and b. On the other hand, the perihelial tuning supplies a pitch even for the aphelial movements of Mars, Mercury, and (relatively speaking) Jupiter, but to the perihelial movements of Jupiter, Venus, and (relatively speaking) Saturn, and to a certain extent to that of the Earth and indubitably to that of Mercury too. For let us suppose that now not the aphelial movement of Venus but the 3´3″ of the perihelial gets the pitch of e; it is approached very closely by the 3´0″ of the perihelial movement of Mercury, through a double octave, at the end of Chapter 4. But if 18″ or one tenth of this perihelial movement of Venus is subtracted, 2´45″ remains, the perihelion of Jupiter, which occupies the pitch of d; and if one fifteenth or 12″ is added, the sum will be 3´15″, approximately the perihelion of Mars which occupies the pitch of f; and thus in b, the perihelial movement of Saturn and the aphelial movement of Jupiter have approximately the same tuning. But one eighth, or 23″, if multiplied by 5, gives 1´55″, which is the perihelial movement of the Earth; and, although it does not square with the foregoing in the same scale, as it does not give the interval 5 : 8 below e nor 24 : 25 above G, nevertheless if now the perihelial movement of Venus and so too the aphelial movement of Mercury, outside of the order, occupy the pitch e-flat instead of e, then there the perihelial movement of the Earth will occupy the pitch of G, and the aphelial movement of Mercury is in concord, because 1´1″, or one third of 3´3″, if multiplied by 5, gives 5´5″, half of which, or
[paragraph continues] 2´32″, approximates the aphelion of Mercury, which in this extraordinary adjustment will occupy the pitch of c. Therefore, all these movements are of the same tuning with respect to one another; but the perihelial movement of Venus together with the three (or five) prior movements, viz., in the same harmonic mode, divides the scale differently from the aphelial movement of the same in its tuning, viz., in the major mode [denere duro]. Moreover, the perihelial movement of Venus, together with the two posterior movements, divides the same scale differently, viz., not into concords but merely into a different order of concords, namely one which belongs to the minor mode [generis mollis].
But it is sufficient to have laid before the eyes in this chapter what is the case casually, but it will be disclosed in Chapter 9 by the most lucid demonstrations why each and every one of these things was made in this fashion and what the causes were not merely of harmony but even of the very least discord.
Footnotes
1034:3 See note to Intervals Compared with Harmonic Ratios, p. 1026.
1035:1 The table is as follows:
1037:1 Natural song: music in the basic major or minor system without accidentals. E. C., Jr.
















